氣體離心機二維供料射流流場的數值模擬

姜東君 　王黎明 　曾實

(清華大學工程物理系  北京100084)

    摘要：為研究氣體離心機供料射流的流動狀況,采用數值求解二維Navier-Stokes方程組的方法對其進行了模擬,計算得到了不同供料角度下的流場分布。結果表明,供料射流對離心機流場在徑向和軸向上的分布都有影響;供料角度為0°時,氣體在軸向上反復膨脹、壓縮,形成膨脹波和激波,對徑向的影響較小;供料角度為45°和90°時,射流對軸向的影響減弱,對徑向流動的影響顯著增強。由計算結果可知,離心機環流的計算中應當對供料條件進行修正。

    關鍵詞：供料射流;離心機;二維Navier-Stokes方程組;激波

    中圖分類號:O35文獻標識碼:A文章編號:1000-0054(2008)08-1287-03

    為了提高氣體離心機的分離性能,通常在其內部引入二次環流[1]。供取料驅動是較為常用的驅動方式,由于取料口位于離心機側壁附近,因此關于取料對二次環流影響的研究比較深入,對取料器附近流場的研究也比較多[2-4],而對位于中心區域的供料射流的研究相對較少。由于供料射流影響離心機內部流場的粘性邊界,因而對環流的影響也必須加以考慮。在以前的研究中,供料驅動條件往往是根據供料量和一定的假設在粘性邊界上給出的,如采用均勻亞聲速流動條件[5],或者采用滿足一定函數分布的源項[6]。以上各種假設不能夠反映真實的流動狀況,因此,有必要對氣體離心機供料射流進行研究。

    離心機內的供料射流同工程中遇到的射流問題有較大不同,工程中射流的周圍為均勻流場,在沒有供料射流時,離心機內的流場滿足旋轉剛體假設[1],即壓強和密度在徑向上呈指數分布,速度為線性分布,當工作氣體射入離心機后,將受到強旋流場的影響,一方面受徑向壓強梯度的影響,在徑向上的膨脹波被壓縮;另一方面受到旋轉的影響而具有角向動量。

    本文通過數值求解二維軸對稱Navier-Stokes方程組,模擬離心機內的二維軸對稱供料射流流場,并對不同供料角度下的流場進行了分析,為實際離心機供料射流流場的研究打下了基礎。

    1　計算模型

    在本文的計算中,離心機參數按照Iguacu模型[5]給定,其轉子半徑為6cm,長徑比為8,側壁線速度為600m/s,即旋轉角速度為104rad/s,側壁壓強為13.3kPa。采用二維軸對稱供料模型,如圖1所示。本文計算了3種供料模型,其區別在于射流角度的不同,如圖1a、1b和1c所示,射流角度α分別為0°、45°和90°。

    2　計算方法

    2.1　控制方程控制方程為二維軸對稱Navier-Stokes方程組:

    由于在射流出口為超聲速,流動為紊流狀態,在計算中選用Realizablek-ε湍流模型。

    2.2　計算方法

    在計算中采用有限體積法對控制方程進行離散,計算中使用二階迎風格式,隱式迭代。

    3　邊界條件和初始條

    件離心機處于高速旋轉狀態,因此在計算中采用旋轉坐標系,旋轉角速度為1×104rad/s。

    計算中用到的邊界如圖1所示,具體設置如下。

    供料入口:給定來流的壓強、速度和溫度。

    轉子側壁:旋轉壁面,給定壁面的旋轉速度(600m/s)和溫度(300K)。

    壓力出口:按照剛體旋轉條件[1]設定背壓:

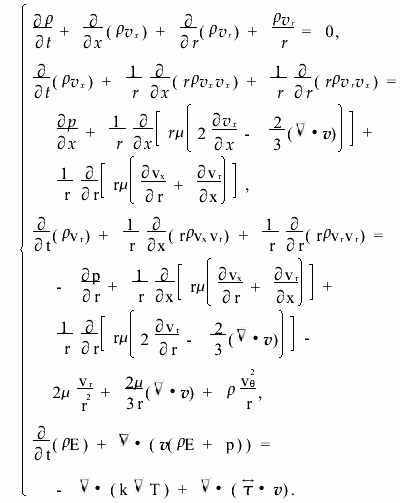
    底部端蓋:旋轉的壁面條件,給定壁面的旋轉速度和溫度。

    在計算中,以無供料時的離心機流場(即旋轉剛體假設)作為初場,壓強分布見式(1),密度為

    4　計算結果及分析

    計算中使用的氣體為UF6,其相對分子量為352。入口條件給定為500Pa,溫度為300K,速度為0。在此供料條件下,計算得到了射流角度分別為0°、45°和90°3種供料模型的流場。

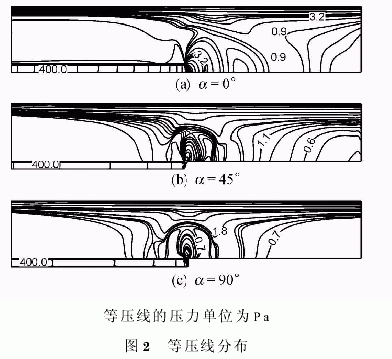
    圖2給出了3種供料模型下的等壓線分布,相應的等馬赫數線分布如圖3所示。在供料角度為0°情況下,當氣體進入離心機后,迅速膨脹,在徑向上受到離心機壓力梯度的影響,被迅速壓縮;在軸向上存在壓縮-膨脹-再壓縮-再膨脹的過程。當供料角度為45°時,氣體在徑向上的膨脹壓縮過程較為明顯,軸向上的分布已經明顯減弱。在供料角度為90°的情況下,氣體在進入離心機內之前,在管口處形成了激波,經過激波后,氣體的速度明顯降低,可以看到,形成的膨脹-壓縮波基本上是以出口為中心的圓弧,在軸向上呈對稱分布,與供料角度為45°的情況相比,對離心機側壁處的影響減弱。在圖3中可以觀察到同樣的流動現象。

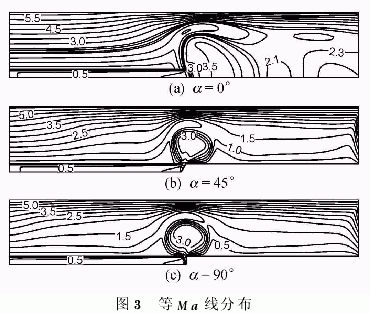
    對于不同的供料模型,圖4分別給出了在半高處(x=0.24m)徑向上的Ma分布。從圖中可以看到,在r=0.04～0.06m之間,在0°供料角條件下,Ma基本保持線性分布;供料角為45°和90°兩種情況下,Ma的分布基本相同,也呈線性分布,但其分布曲線位于供料角為0°的曲線下方。這表明當供料角度增大后,徑向速度增大,從而對離心機流場施加了更大的影響。

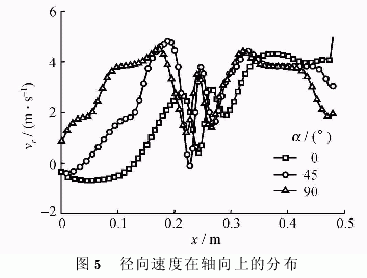
    供料射流對離心機流場的最主要影響是對近側壁處環流的干擾,因此環流計算內邊界處,軸向和徑向速度在軸向上的分布是本文所關心的。圖5和圖6給出了半徑r=0.048m處軸向上的徑向和軸向速度分布曲線,從中可以觀察到,對于文中計算的3種供料條件,徑向速度在軸向上的分布比較復雜,在3種供料角度下,都存在不均勻分布。但一般離心機環流計算經常是將供料假設為一股均勻的亞聲速流動,這是應當修正的。在供料角為45°和90°時,軸向速度則基本上以半高處為中心對稱分布。

    5　結論和討論

    本文通過求解二維軸對稱Navier-Stokes方程組模擬了二維離心機射流流場,采用有限體積法離散,使用二階隱式迎風格式迭代計算,得到了不同供料角度下的流場分布。對計算結果的分析表明:

    1)射流對離心機流場在徑向上和軸向上的分布都有影響;

    2)在供料角度為0°時,氣體在軸向上反復膨脹、壓縮,對徑向上的流場影響較小;

    3)在供料角為45°和90°時,射流對軸向的影響減弱,對徑向流動的影響顯著增強;

    4)無論在何種供料條件下,供料射流所造成的流動參數(包括徑向速度和軸向速度)在軸向上的變化,在離心機環流計算中都應當被考慮。

    本文計算的是二維情況下供料射流對離心機流場的影響,實際的供料模型更為復雜,需要進行三維數值模擬。